离散数学-等价关系与偏序关系

等价关系

定义

设存在关系R，若R满足：

1. R是A上的二元关系
2. R是自反、==对称==、传递关系
   则，R为A上的等价关系。

例子

1. 如果同年龄的大学生认为是相关的，不同年龄的大学生是无关的，则这种年龄关系R是等价关系
2. 如果姓氏相同的的大学生认为是相关的，不同姓氏的大学生是无关的，则这种姓氏关系R是等价关系

综上，若对于一个集合A种的元素，按某种条件进行分组，并使得：

1. A种每个元素必属于某一组且仅属于一组
2. 定义同一组内的元素相关，不同一组内的元素无关
   则定义的二元关系必然是等价关系

特征

若把A中的元素按“组”顺序排列，那么等价关系R的关系矩阵是由若干个元素全为1的小方阵构成

等价类和商集

定义

等价类

设R是A商的等价关系，a是A中的任意元素，由A中所有与a相关的元素组成的集合，称为a关于R的等价类，记作$[a]_R$

商集

设R是A上的等价关系，由关于R的所有不同的等价类作为元素构成的集合称为A关于R的商集，记作A/R

集合划分

定义

设A是集合，$A_1 , A_2 , \dots , A_n$ 是A的非空子集，且满足：

1. $A_1 \cup A_2 \cup \dots \cup A_n = A$
2. $A_i \cap A_j = \emptyset(i \neq j,i,j = 1,2,3,\dots,n)$

则以$A_1 , A_2 , \dots , A_n$作为元素构成的集合S称为集合A的划分，每个子集$A_i$称为块

等价类、商集与集合划分

当R是A上的等价关系时，A关于R的商集时A的一个划分，等价类就是块

于是有定理：

集合运算的等价关系

设$R_1$ 和 $R_2$ 时非空集合A上的等价关系，则

1. $R_1 \cup R_2$ 一定不是等价关系
2. $R_1 \cap R_2$ 一定是等价关系
3. $R_1 - R_2$ 一定不是等价关系
4. $R_1 \oplus R_2$ 一定不是等价关系

可通过定义法，验证是否满足转递、自反、对称关系证明

偏序关系

定义

设有关系R，集合A，若R满足：

1. R是A上的二元关系
2. R是自反，==反对称==，传递关系

则R是A上的偏序关系(半序关系)

例子

1. 对于正整数集，$\mathbb{Z}^+$,R是其上的小于等于关系关系，即当$a \leq b$时，$(a,b) \in R$，则R是其上的偏序关系
2. 对于正整数集，$\mathbb{Z}^+$,R是其上的整除关系，即当$b \ mod \ a = 0$时，$(a,b) \in R$，则R是其上的偏序关系

通常把集合A和集合A上的偏序关系R合在一起称为偏序集，并记作（A,R）或（A,$\preceq$）

偏序关系哈斯图表示

由偏序关系的特征：

1. 每个顶点都有自回，则可省略所有自环
2. 对于$(a,b) \in R$和$(b,c)\in R$时，必有$(a,c) \in R$，则可省略a到c的边
3. 通过调整点的位置，可以使所有有向边全部朝上，则可省略有向边的箭头

例子

如设A = {1,2,3,4,5,6,12},R时A上的整除关系。易知，R = {(1,1),(2,2),(3,3),(4,4),(6,6),(12,12),(1,2),(1,3),(1,4),(1,6),(1,12),(2,4),(2,6),(2,12),(3,6),(3,12),(4,12),(6,12)}

则使用有向图表示为：

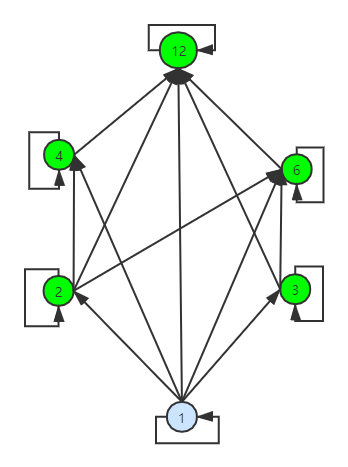
使用哈斯图表示为：

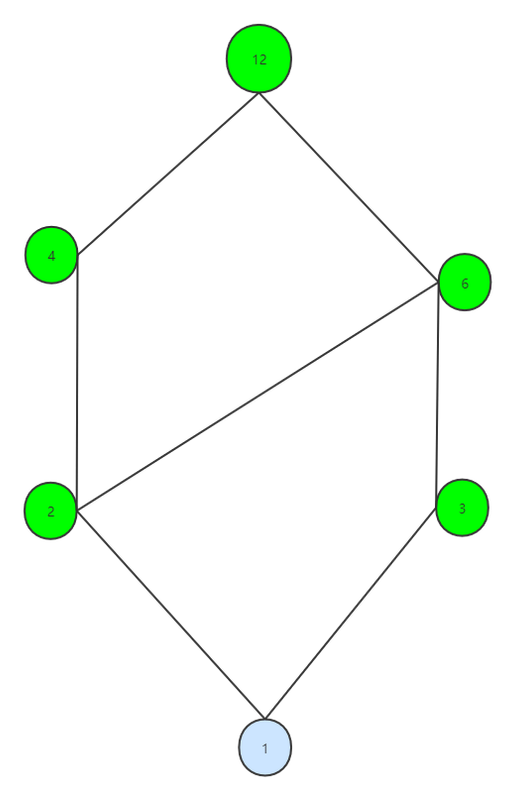
覆盖

设A(A,$\preceq$)是偏序集，a和b是A种两个不同的元素，如果$a\preceq b$，且在A中不存在其他元素c，使得$a\preceq c,c\preceq b$，则称b覆盖a

作图原则

利用覆盖的概念，可以油邻接矩阵直接画出哈斯图，即：

当b覆盖a时，代表b的顶点应华仔代表a的顶点上复，并用直线段连接这两个顶点

偏序集中的特殊元素

设A(A,$\preceq$)是偏序集，A中存在元素a

1. 极小元：
   1. A中没有其他元素x满足$x\preceq a$，则a为A中的极小元
   2. 即a再也不能==覆盖==A中其他元素时，a时极小元
2. 极大元：
   1. A中没有其他元素x满足$x\succeq a$，则a为A中的极小元
   2. 即A中没有其他元素能==覆盖==a时，a为极大元
3. 最小元：
   1. 中任何元素x，都有$x\succeq a$，则a为A中的最小元
   2. 即能被所有覆盖
4. 最大元：
   1. A中任何元素x，都有$x\preceq a$，则a为A中的最大元
   2. 即能覆盖所有
5. 上界：设B是A的子集，如果B中任何元素x，都有$x\preceq a$,则称a为子集B的上界
6. 下界：设B是A的子集，如果B中任何元素x，都有$a\preceq x$,则称a为子集B的下界
7. 上确界：
   1. 设B是A的子集，a是B的上界，若B中任何上界x，都有$a\preceq x$，则称a为子集B的上确界
   2. 即最小上界
8. 下确界：
   1. 设B是A的子集，a是B的上界，若B中任何上界x，都有$x \preceq a$，则称a为子集B的下确界
   2. 即最大下界

全序集和拟序集

全序集

定义

设A(A,$\preceq$)是偏序集，如果A中任意两个元素都是可比的（即任意两个元素都有关系），则称$\preceq$为全序关系，$(A,\preceq)$为全序集

例子

如$Z^+$是正整数集合，对于先于等于关系，$(Z^+,\preceq)$是全序集下

拟序集

定义

设R是A上的一个二元关系，若满足：

1. R是反自反关系
2. R是传递关系

则R为A上的拟序关系，A为拟序集

例子

如$Z$上的小于关系是拟序关系

相关定理

拟序关系有如下定理：